Simulation & Statistics in R

INTRODUCTION

As a statistician, we Want to deal with random experiments. So to do that, thare are various techniques to predict the outcome of such experiments :

• Wait and See: Designing winning strategies by trial-and-error method.

• Solving Probability Models: Assume a definite mathematical model to predict outcome, sometimes gets complicated.

• Simulate Probability Models: Also start with a mathematical model, but instead of computing it mathematically we use computers to perform the virtual random experiment following that model and then analyze the artificial data generated by computers. Similar to “wait and see” except that we do not need to wait long reality.

Concept Of Simulation

• Assume a mathematical model.

• Use computers to perform the random experiment artificially.

• Computers can do artificial random experiment as computers can generate random numbers.

• Use the artificial data generated by the computers to analyze the model and predict the outcome.

• Note that, the random numbers generated by computers are not random in absolute sense, they are only pseudo-random numbers.

Why do we simulate ?

• To have a better understanding of the known probability models.

• To visualize a probability model with examples of outcome of a random experiment ( which in reality are hard to obtain )

• To have an idea about the result of a statistical model which cannot be solved explicitly using formula.

• To judge the performance a model before applying it to a real data situation.

Drawing of Simple Random Sample

• We use the sample() command for both with-replacement & with-out-replacement sampling.

set.seed(123)
sample(c("A","B","C","D","E"),size = 3,replace = F) #-- Without replacement

## [1] "C" "B" "E"

set.seed(123)
sample(c("A","B","C","D","E"),size = 3,replace = T) #-- With replacement

## [1] "C" "C" "B"

Example

set.seed(5)
sample(1:10,size=2,replace = T)

## [1] 2 9

set.seed(6)
sample(100,size=5)

## [1] 53 10 45 78 56

Unequal Probability Sampling

set.seed(7)
sample(c("A","B","C"),size = 2,prob = c(0.1,0.4,0.5))

## [1] "A" "C"

Similating Coin Tosses

• An unbiased coin is tossed 10 times. Lets see the output of the tosses.

set.seed(100)
sample(c("H","T"),10,replace = T)

##  [1] "T" "H" "T" "T" "H" "H" "T" "T" "T" "H"

• Suppose now the probability of head is 2/6

set.seed(100)
sample(c("H","T"),10,replace = T,prob = c(2/6,4/6))

##  [1] "T" "T" "T" "T" "T" "T" "H" "T" "T" "T"

Find the Proportion of heads & tails in long run

prop=NULL
size1=seq(100,10000,by=1000)
size2=seq(20000,500000,by=10000)
size=c(size1,size2)
for (n in size)
{
  x=sample(0:1,n,rep=T)
  prop=c(prop,sum(x)/n)
}
plot(size,prop,type="l")
abline(0.5,0)

Find the Proportion of heads & tails in long run

##  [1]    100   1100   2100   3100   4100   5100   6100   7100   8100   9100
## [11]  20000  30000  40000  50000  60000  70000  80000  90000 100000 110000
## [21] 120000 130000 140000 150000 160000 170000 180000 190000 200000 210000
## [31] 220000 230000 240000 250000 260000 270000 280000 290000 300000 310000
## [41] 320000 330000 340000 350000 360000 370000 380000 390000 400000 410000
## [51] 420000 430000 440000 450000 460000 470000 480000 490000 500000

##  [1] 0.4800000 0.5100000 0.4985714 0.4880645 0.5026829 0.4905882 0.5039344
##  [8] 0.5021127 0.5004938 0.5057143 0.4978500 0.5019333 0.5033500 0.5027600
## [15] 0.5003167 0.5004000 0.4984125 0.5031000 0.4990700 0.4997818 0.4995667
## [22] 0.4988692 0.5021143 0.5017067 0.5019000 0.4986529 0.5001111 0.5005684
## [29] 0.5001250 0.4984714 0.4992182 0.4990478 0.4965500 0.4987200 0.4986769
## [36] 0.4991741 0.4989179 0.5002103 0.4991067 0.4998323 0.5003156 0.4998909
## [43] 0.4985824 0.4995286 0.5017111 0.5003432 0.4990737 0.5005205 0.4994575
## [50] 0.4997585 0.4988833 0.4997023 0.5001773 0.5009356 0.5003457 0.5004979
## [57] 0.5000729 0.4997633 0.4996940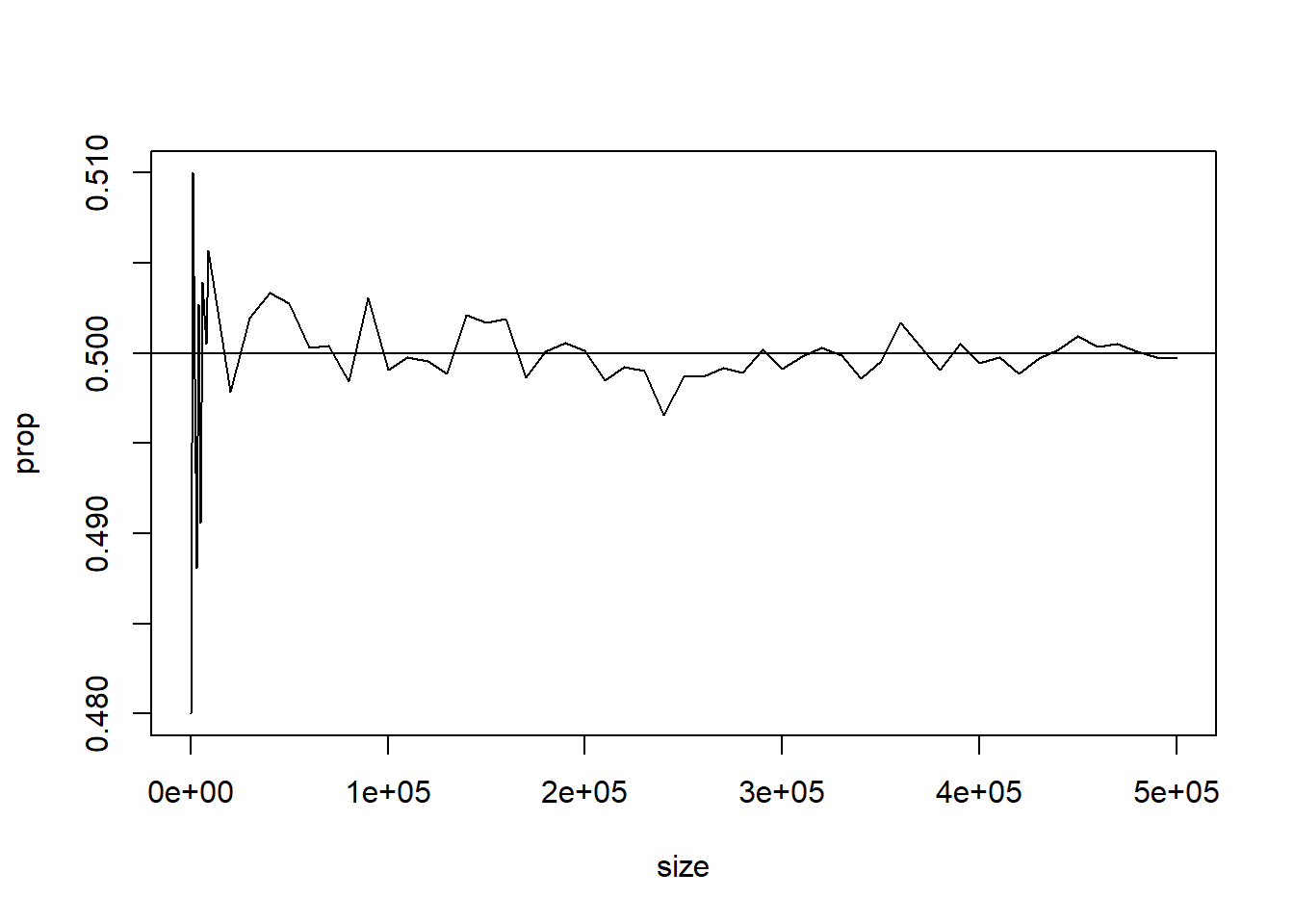

Finding Probabilities

Drawing a Card

• A card is drawn from a full pack of 52 cards. Find the probability that the drawn card is a picture card (i.e., king, queen or jack).

set.seed(125)
pic=NULL
for(i in 1:10000)
{
  x=sample(52,size = 1)
  if(any(x%%13==c(11,12,0)))
  {
    pic[i]=1
  }
  else pic[i]=0
}
sum(pic)/10000

## [1] 0.2287

• Because, king= ${11}^{th}$ no. card, queen=${12}^{th}$ no. card,jack=${13}^{th}$ no. card.

Divisibility Test

• A number is chosen at random from 1 to 1000. Find the probability that it is divisible by 3, 5 or 6.

count=0
for(i in 1:100000)
{
  num=sample(1000,1)
  if(num%%3==0||num%%5==0||num%%6==0)
  {
    count=count+1
  }
}
count/100000

## [1] 0.46794

Urn-Ball Problem

• Suppose an urn contains 7 white and 5 black balls. 3 balls are chosen at random without replacement. Find the probability that :
  • all the 3 balls are white
  • 2 are white and 1 is black.

Urn-Ball Problem

count1=0; count2=0
balls= as.factor(c(rep("W",7),rep("B",5)))
for ( i in 1:10000)
{
chosen= sample(balls,3)
if (all(chosen=="W")) count1=count1+1
if (table(chosen)["W"]==2) count2=count2+1
}
count1/10000; count2/10000

## [1] 0.1565

## [1] 0.4859

Birthday Problem

• In a class of 25 students, find the probability that at least two students share the same birthday.

count=0
for(i in 1:500)
{
  ##-- drawing samples by SRSWR --##
  class=sample(365,25,replace = T)
  if(length(unique(class))<length(class))
  {
    count=count+1
  }
}
count/500

## [1] 0.574

Card Shiffting

• Often we speak of well-shuffled deck of cards.

• When we shuffle a deck by hand, the shuffling is always imperfect (not random)

• We can simulate these imperfect shuffling in computer.

Cut Shuffle

• The simplest method is “cutting” the deck.

• We cut the deck at some random point chosen somewhere around the middle of the deck.

• Then put the lower part on the top of the upper part.

• We shall simulate this shuffle.

Simulating a Cut Shuffle

cut=function(deck)
{
  #choose a random cut point near middle
  x=rbinom(1,52,0.5)
  temp=c(deck[(x+1):52],deck[1:x])
  return(temp)
}
cut(1:52)

##  [1] 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48
## [26] 49 50 51 52  1  2  3  4  5  6  7  8  9 10 11 12 13 14 15 16 17 18 19 20 21
## [51] 22 23

Riffle Shuffle

• A much more reliable way is the rifle shuffle ( also known as Faro shuffle or dovetail shuffle)

• First split the deck into two parts just as in the cut method.

• Take the top half in left hand, and the other half in your right.

• Release the cards randomly from both the hands.

• Mathematically, if at any stage there are $a$ cards in your left hand and $b$ cards in your right, then the next card comes from the left hand with probability $\frac{a}{a+b}$ and from the right with probability $\frac{b}{a+b}$.

Simulating Riffle Shuffle

riffle=function(deck)
{
  n=length(deck)
  x=rbinom(1,52,0.5)
  
  left=deck[1:x]; right=deck[(x+1):52]; k=0;
  
  a=length(left); b=length(right); tab=NULL;
  
  for(i in 1:52 )
  {
    ind=rbinom(1,1,a/(a+b))
    
    if(ind==1)
    {
      tab[k+1]=left[a]
      
      left=left[1:(a-1)]
      
      k=k+1; a=a-1
    }
    else
    {
      tab[k+1]=right[b]
      
      right=right[1:(b-1)]
      
      k=k+1; b=b-1
    }
  }
  return(tab)
}

Simulating Riffle Shuffle

riffle(1:52)

##  [1] 26 52 25 51 50 49 48 24 23 22 21 20 47 19 18 46 17 16 45 15 44 43 14 42 41
## [26] 40 39 13 12 11 38 10  9  8  7 37  6 36 35 34 33  5  4 32  3 31 30  2 29 28
## [51] 27  1

Simulating Random Variables

• We can simulate a Uniform(0,1) variable by the command runif()

• This can be used to generate random variables from other discrete and continuous as well.

• Suppose we want to generate a Bernoulli random variable with probability of success 0.7

bernoulli=function(prob)
{
  u=runif(1); x=NULL;
  if(u<prob) x=1
  else x=0
  return(x)
}

bernoulli(0.7)

## [1] 0

Using it farther

• Suppose we want to simulate a Geometric(0.8) random variable.

x=1
y=bernoulli(0.8)
while(y!=1)
{
  y=bernoulli(0.8)
  x=x+1
}
x

## [1] 1

Much Complicated Ones

• How can we generate poisson or a Hypergeometric random variable using the above technique ?

• For this we need to take the help of the following fact :

Generating Poisson Distribution

poi_mass=function(x,lambda)
{
  return(exp(-lambda)*(lambda^x)/factorial(x))
}

poi_sample=function(lambda)
{
  U=runif(1); i=0; cumprob=poi_mass(0,lambda)
  
  while(U>cumprob)
  {
    i=i+1
    cumprob=cumprob+poi_mass(i,lambda)
  }
  return(i)
}
poi_sample(5)

## [1] 2

Continuous Distributions

• For continuous distributions we use the following fact :

Working with inbuilt R functions

• Suppose we want to generate random variables from $N(\mu ,{\sigma }^2)$

# 2 samples from N(5,2) Distribution
rnorm(n=2,mean=5,sd=sqrt(2))

## [1] 7.280889 6.274643

• Now let us find $P(X\le x)$ i.e., $\mathrm{\Phi }(\frac{x-\mu }{\sigma })$

# P(X<=4) for N(5,2)

pnorm(4,mean=5,sd=sqrt(2))

## [1] 0.2397501

# P(X>7) for N(5,2)

pnorm(7,mean=5,sd=sqrt(2),lower.tail = F)

## [1] 0.0786496

• We can also compute the normal quantiles $z_{\alpha }$

# lower 0.05 point

qnorm(0.05,mean=5,sd=sqrt(2))

## [1] 2.673826

# lower 0.01 point

qnorm(0.01,mean=5,sd=sqrt(2),lower.tail = F)

## [1] 8.289953

• Can also compute normal density $\varphi (\frac{x-\mu }{\sigma })$

# density at x=2

dnorm(2,mean = 5,sd=sqrt(2))

## [1] 0.02973257

# density at x=5
dnorm(5,mean=5,sd=sqrt(2))

## [1] 0.2820948

Plotting the normal density

x=seq(-3,3,by=0.01); y=dnorm(x,0,1)
plot(x,y,type="l",main="Density of N(0,1)",ylab=expression(phi(x)))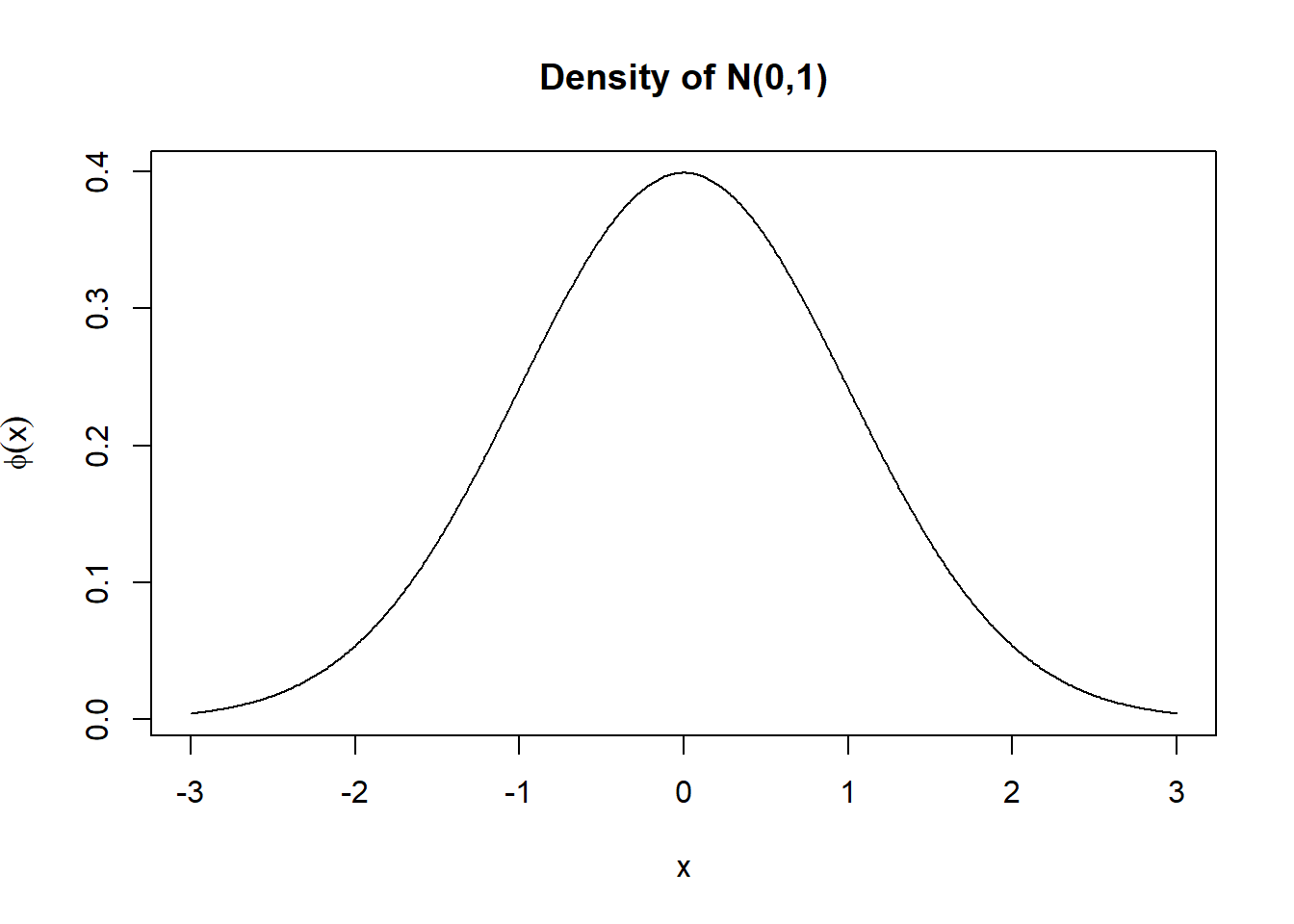

Other Standard Distributions in R

Central Limit Theorem

n=100
k=10000
U=runif(n*k)
M=matrix(U,n,k)
X=apply(M,2,sum)
Z=(X-n/2)/sqrt(n/12)
par(mfrow=c(1,2))
hist(Z)
qqnorm(Z)
qqline(Z,col="red")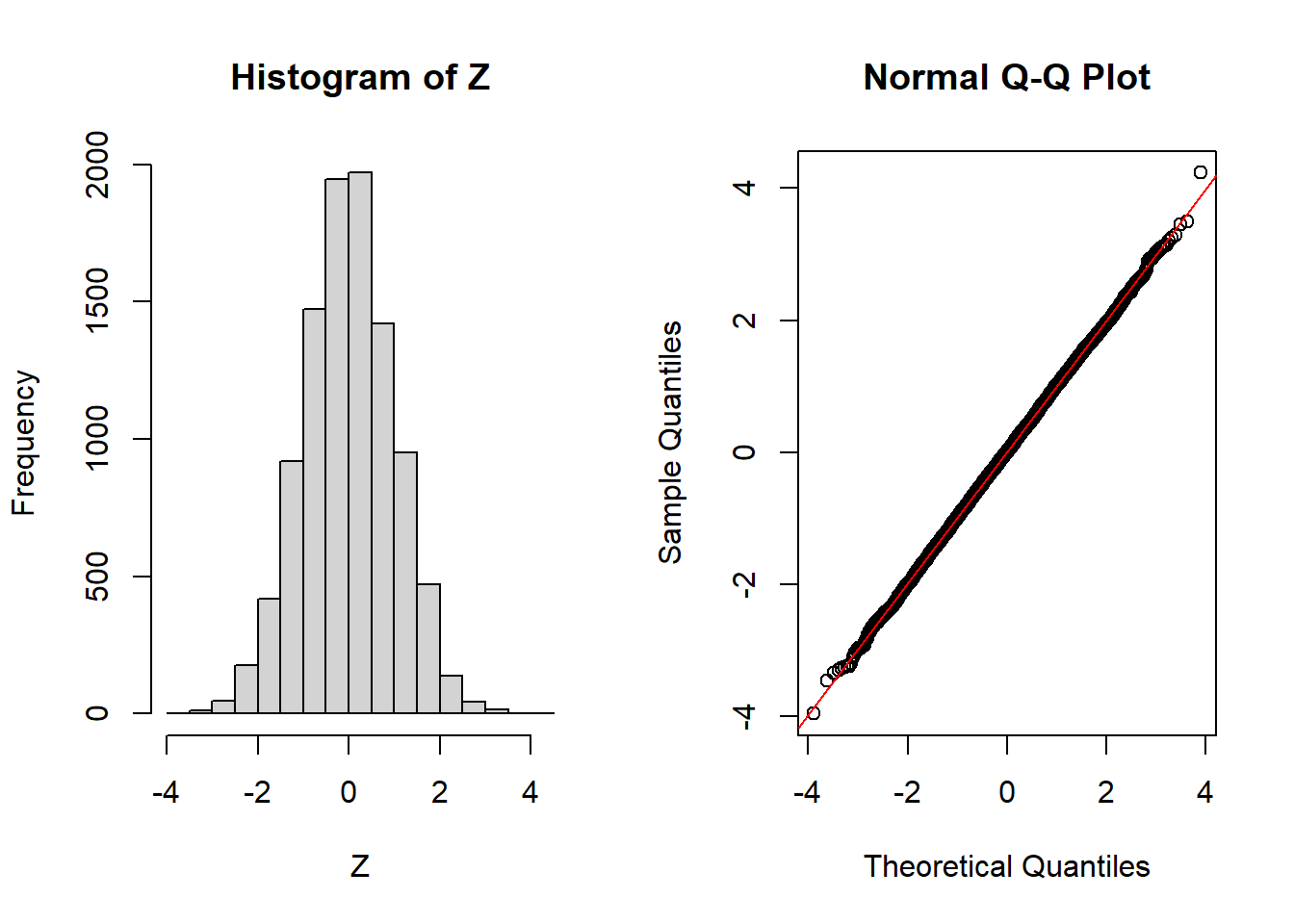

Law of Laege Numbers

• The weak Law of large numbers says that for any $ϵ>0$ the sequence of probabilities $$P(|\frac{S_n}{n}-\mu |<ϵ)⟶1asn⟶\mathrm{\infty }$$

• Consider i.i.d. coin flips, that is, Bernoulli trials with $p=\mu =\frac{1}{2}$

• We find the $P(|\frac{S_n}{n}-\mu |<ϵ)$ in R and illustrate the limiting behavior, with $ϵ=0.01$

Plotting the Probability

wlln=function(n,eps,p)
{
  pbinom(n*p+n*eps,n,p)-pbinom(n*p-n*eps,n,p)
}
prob=NULL
for(n in 1:10000)
{
  prob[n]=wlln(n,eps=0.01,p=0.5)
}
plot(prob,type="l",xlab="n",ylab=expression(P(X<=x)))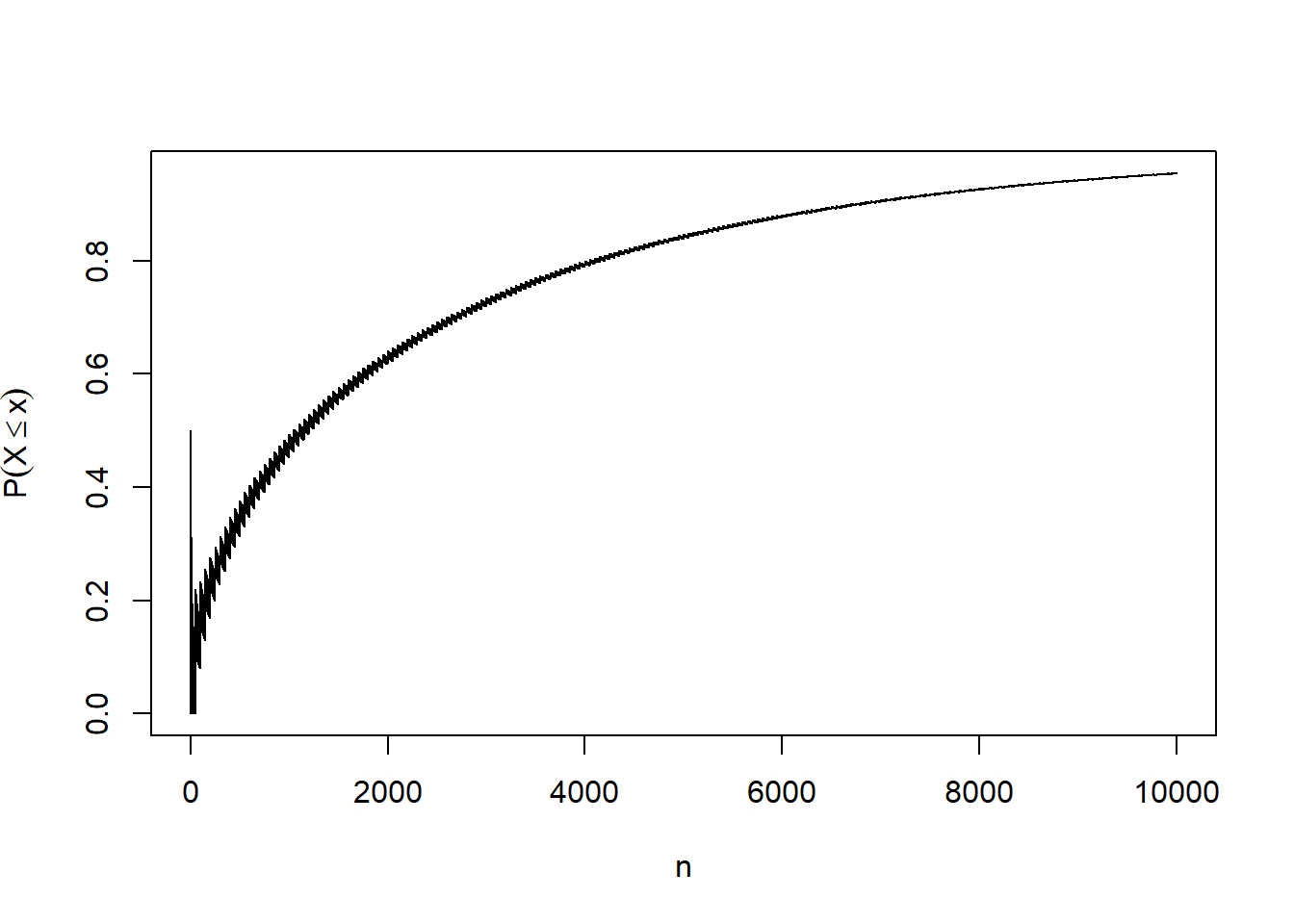

Strong Law of large numbers

• The strong law of large numbers says that $\frac{S_n}{n}⟶\mu w.p.1;asn⟶\mathrm{\infty }$

• Consider i.i.d. coin flips, that is, Bernoulli trials with $p=\mu =\frac{1}{2}$

• The sum $S_n$ is a Binomial random variable.

Illustrating Strong Law

slln=function(n,p)
{
  x=rbinom(1,size=n,prob=p)
  return(x)
}
value=NULL
for(i in 1:10000)
{
  value[i]=slln(i,0.5)/i
}
plot(value,type="l",xlab="n",ylab="Sample mean")
abline(h=0.5)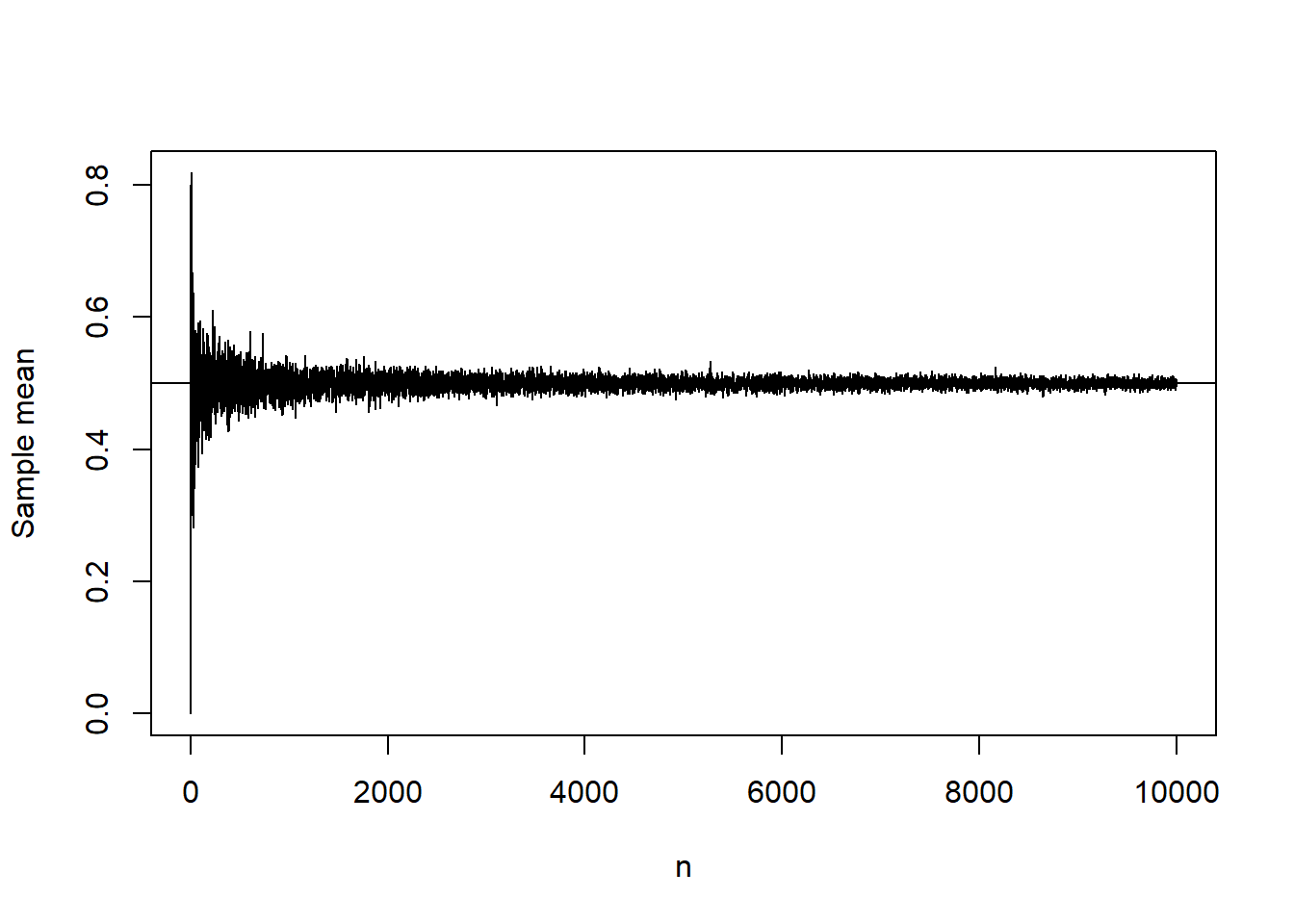

Family Planning

• Suppose a couple is planning to have children until they have one child of each sex. Assuming male and female child are equally probable, how may children can they expect to have ?

count=NULL
for(i in 1:1000)
{
  child=sample(c(0,1),1)
  while(length(unique(child))<2)
  {
    child=c(child,sample(c(0,1),1))
  }
  count[i]=length(child)
}
mean(count)

## [1] 3.08

Using Simulation to construct Tests

• Simulation can be used to construct tests in situations where the exact sampling distribution of the test statistic is hard to find even under the null hypothesis.

• More specially we use simulation to find the $\alpha 100$% cut-off points

• Suppose we have a sample of 101 from Beta(5,b)

• We want to test $H_0:b=5$ against $H_1:b<5$

• To get an idea about the nature of the test we plot the density function for different values of b.

Plot of Beta Densities

par(mfrow=c(1,3))
x=seq(0,1,by=0.01)
y1=dbeta(x,shape1 = 5,shape2 = 2)
y2=dbeta(x,shape1 = 5,shape2 = 5)
y3=dbeta(x,shape1 = 5,shape2 = 10)
plot(x,y1,type="l",xlab="b<5")
abline(v=median(rbeta(101,shape1 = 5,shape2 = 2)),col="red")
plot(x,y2,type="l",xlab="b=5")
abline(v=median(rbeta(101,shape1=5,shape2=5)),col="red")
plot(x,y3,type="l",xlab="b>5")
abline(v=median(rbeta(101,shape1=5,shape2=10)),col="red")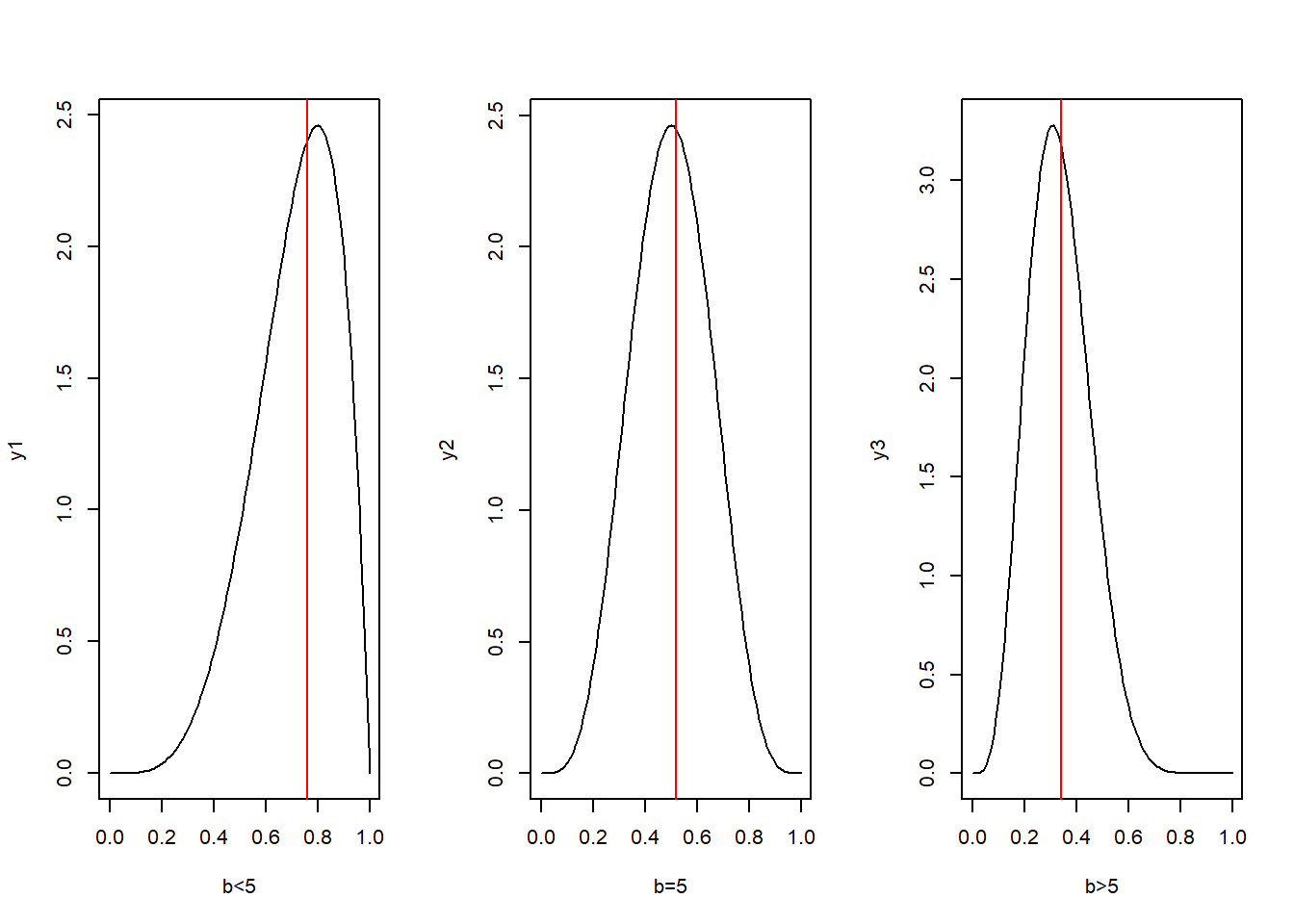

What type of test shall we perform ?

• From the figures we see that sample median can be used as a test statistic.

• Also a right tailed test based on the median will be appropriate

• Thus we shall reject $H_0$ if the sample median exceeds some value $c$.

• We want to find the test at 90% level of signficance.

• We shall use simulation technique to find the cut-off point $c$.

set.seed(100);prob=NULL; j=1
C=seq(0.2,0.9,by=0.001)
for ( c in C)
{
prob[j]=0
for(i in 1:100)
{
x=rbeta(101,shape1=5,shape2=5)
me=median(x)
if(me>c) prob[j]=prob[j]+1
}
prob[j]=prob[j]/100
j=j+1
}
plot(C,prob,type="l")
abline(h=0.9,col="red")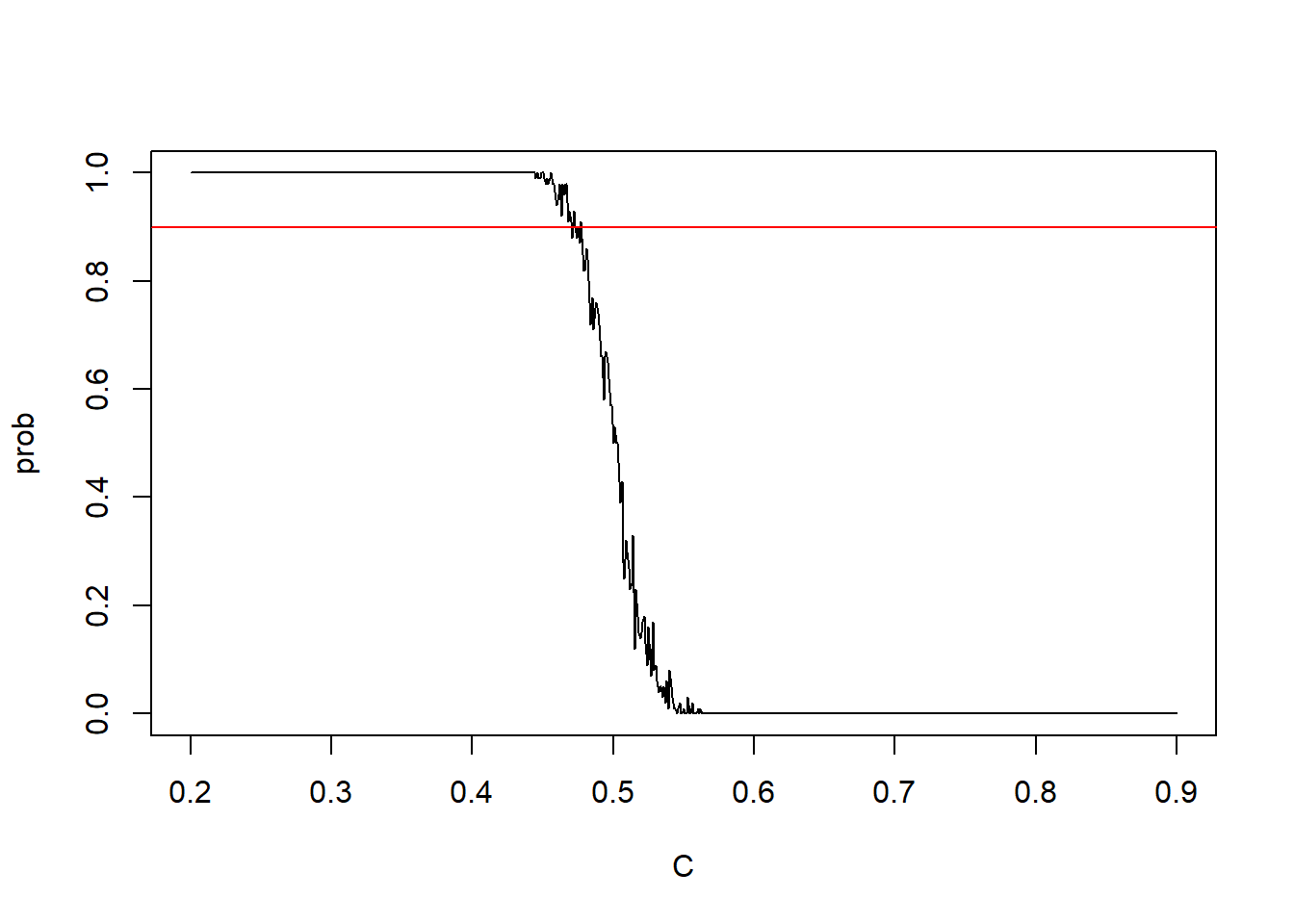

Now lets find the c

We continue to search the c for which $P_{H_0}(me>c)$ is closet to 0.9

C[which(prob>0.89 & prob<0.91)]

## [1] 0.473 0.475

prob[which(C %in% C[which(prob>0.89 & prob<0.91)])]

## [1] 0.9 0.9

So, we can take c to be 0.473 Thus our test rule is: Reject $H_0$ if sample median exceeds 0.473

Generating Normal Variables

• Instead of using R inbuilt function, rnorm(), we can generate Normal variables from scratch.

normal=function(n)
{
  U1 = runif(n)
  U2 = runif(n)
  C = sqrt(-2*log(U1))
  Z1 = C*cos(2*pi*U2)
  Z2 = C*sin(2*pi*U2)
  return(Z1)
}

n = 100000
Z = normal(n)

hist(Z,prob=T,col=rainbow(12))

#-- note that, rainbow() is a graphical function, which gives multiple color.
curve(dnorm(x),-3,3,
      add=T,lwd=4)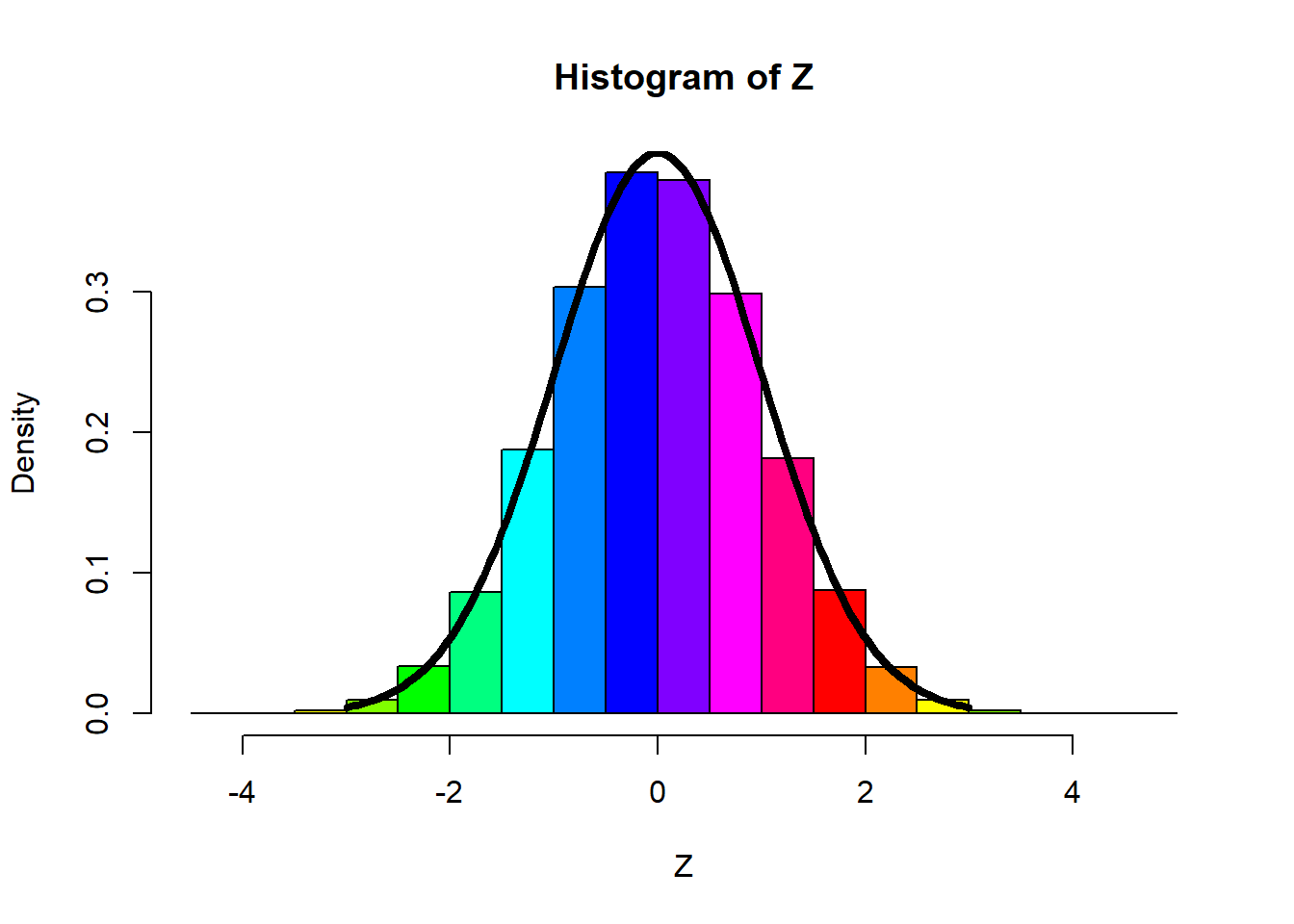

Generating Bivariate Normal Variables

binorm=function(n,rho)
{
  x = numeric(n); y<- numeric(n)
  for (i in 1:n)
  {
    z1 = normal(1)
    z2 = normal(1)
    x[i] = z1
    y[i] = rho*z1+sqrt(1-rho^2)*z2
  }
  return(cbind(x,y))
}
n = 1000 ;rho = -0.5

data = binorm(n,rho)

##-- Plotting Bivariate Normal Data --##

plot(data,
     pch=19,
     xlab="X",
     ylab = "Y")

abline(lm(data[,2]~data[,1]),col="red",
       v=mean(data[,1]),
       h=mean(data[,2]),
       lwd=3)

legend("topright",legend = c(paste("mean(X)= ",round(mean(data[,1]),3)),
                              paste("Var(X)= ",round((sd(data[,1]))^2,3)),
                              paste("mean(Y)= ",round(mean(data[,2]),3)),
                              paste("Var(Y)= ",round((sd(data[,2]))^2,3)),
                              paste("samp corr.= ",round(cor.test(data[,1],data[,2])$estimate,2))),
       cex=0.66)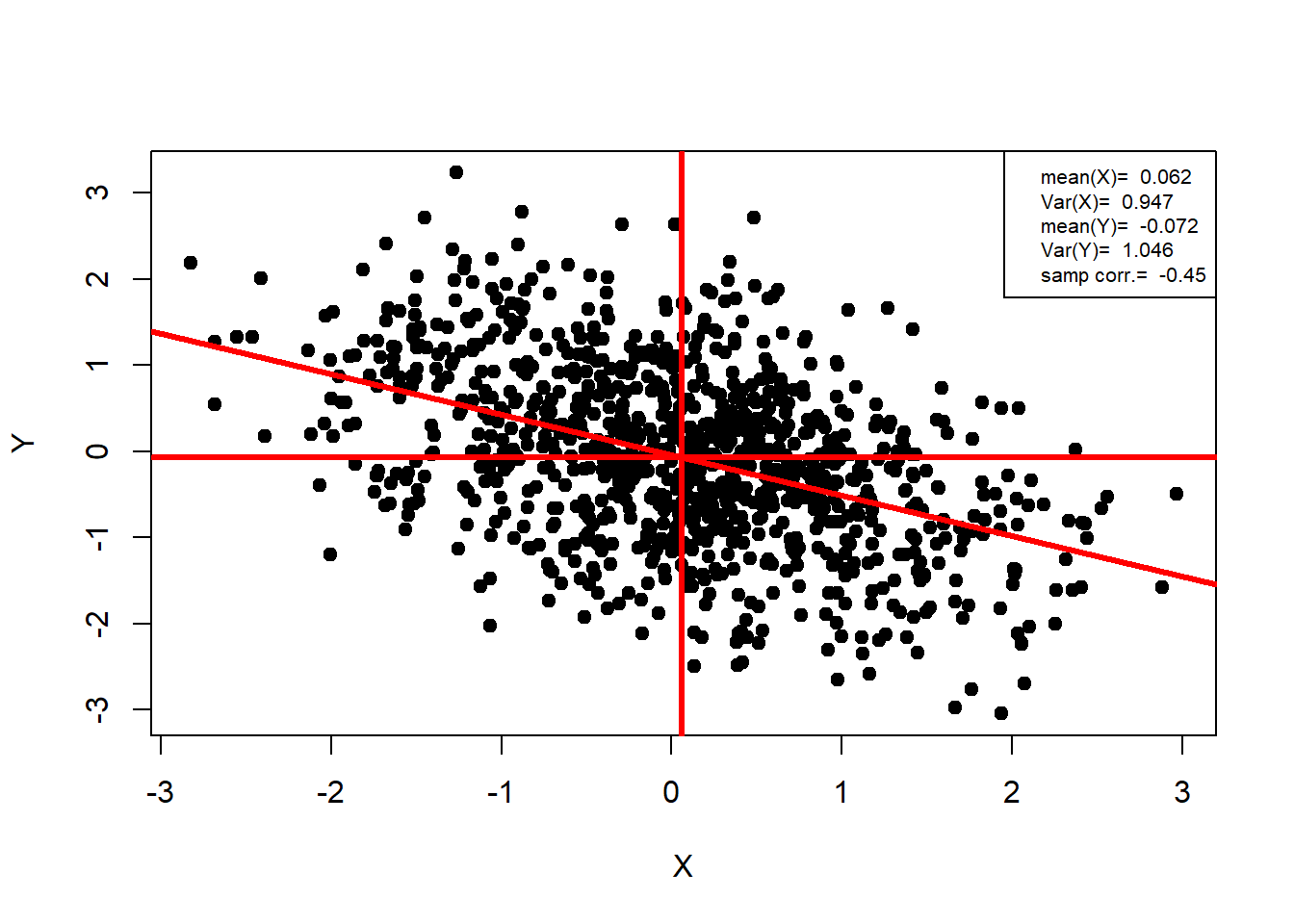

Monte Carlo Simulation

• We know that sample average $\overline{x}$ converges to population mean by consistency property.

• Thus expected value of any function can be approximated by the sample average.

• Thus $\frac{1}{N}\sum _{i=1}^{N}f(X_i)⟶E(f(X))$ with probability 1 as $N⟶\mathrm{\infty }$ if $X_1,X_2,...$ are iid sequence of random variables with the same distribution as $X$.

• A Monte Carlo method for estimating $E(f(X))$ is a numerical method based on the approximation $$Z_N^{MC}=E[f(X)]\approx \frac{1}{N}\sum _{i=1}^N(f(X_1))$$ where $X_1,X_2,...$ are iid sequence of random variables with same distribution as $X$.

Bias & Variance

• The Monte Carlo estimate $Z_N^{MC}$ for $E(f(X))$, has $$bias(Z_N^{MC})=0$$ and $$MSE(Z_N^{MC})=Var(Z_N^{MC})=\frac{1}{N}Var(f(X))$$

Monte Carlo Integration

• Consider the integral ${\int }_a^{b}f(x)dx$

• Objective is to approximate this integral

• Let $X_1,X_2,...$ be iid $U(a,b)$, i.e., density of $X_j$ is $\varphi (x)=\frac{1}{b-a}{I}_{[a,b]}$

• Then $${\int }_a^{b}f(x)dx=(b-a){\int }_a^{b}f(x)\varphi (x)dx=(b-a)E(f(X))\approx \frac{b-a}{N}\sum _{i=1}^{N}f(X_j)$$ for large $N$

set.seed(123)
N = 1000
x = runif(N,min=0,max=(2*pi))
value = sum(exp(cos(x)))
value = (2*pi)*value/N
value

## [1] 7.901431

n = 1000
t = seq(-3,3,0.01)
x = NULL
phi.hat=NULL
phi=NULL
for(i in 1:length(t))
{
 x = rnorm(n)
 s = sum(x<=t[i])
 phi.hat[i] = s/n
 phi[i] = pnorm(t[i])
}
par(mfrow = c(1,2))
plot(t,phi,main="Original c.d.f",col="red",pch=19)
plot(t,phi.hat,main="Estimated c.d.f",col="blue",pch=19)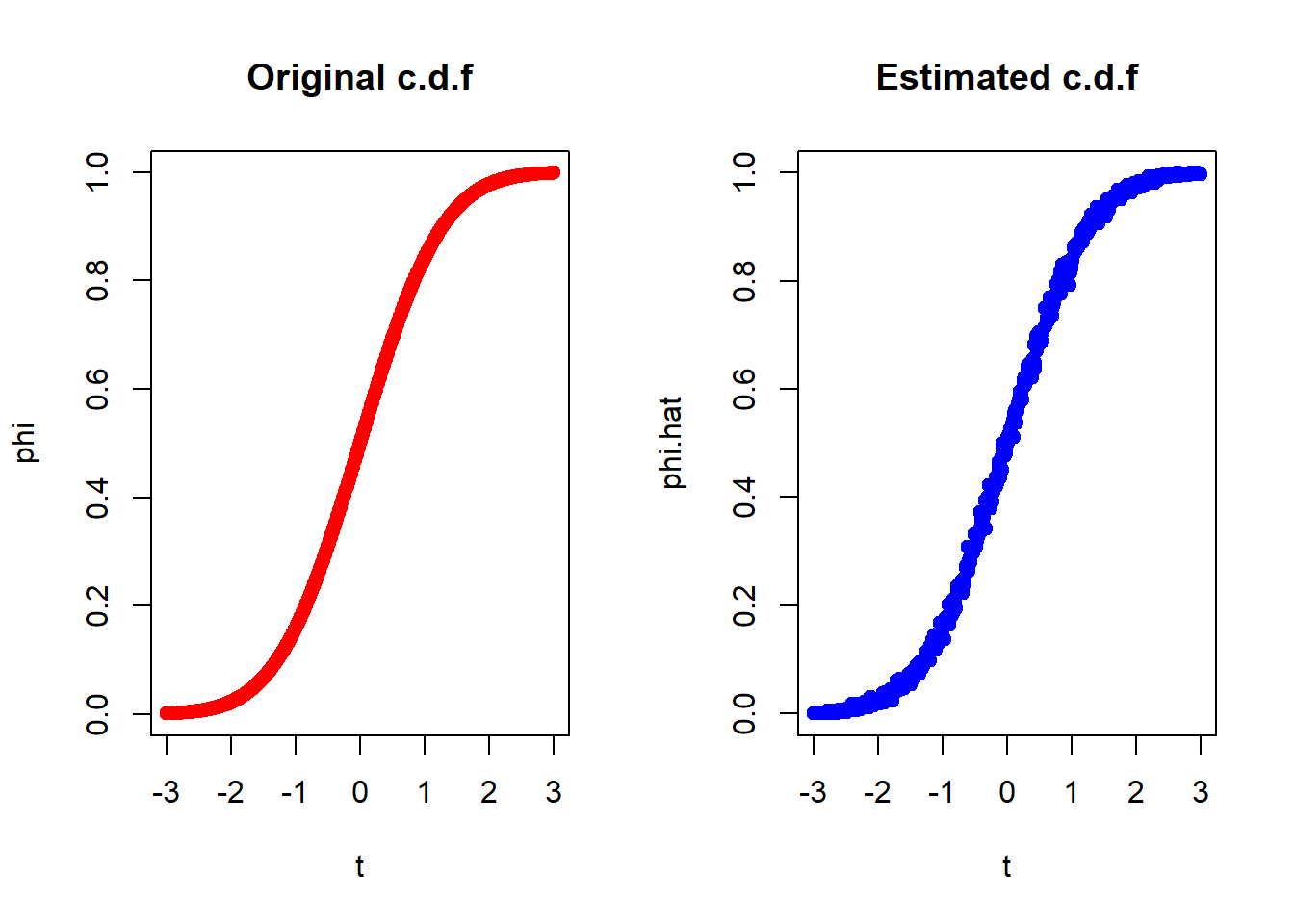

An assignment Problem

Here, we have to do :

• Draw a random sample of size 50 from $N(1,2)$

• Draw another radom sample of size 1000 from the same distribution $N(1,2)$

• Calculate the test statistic :$T_n=\frac{\sqrt{n}(\overline{X_n}-1)}{s_n}$

• Repeat this 1000 times.

• Draw histograms of the $T_n$’s coming from two different samples of the same population $N(0,1)$

• Copare these two histograms with the Standard Normal distribution.

Solution:

• here, to plot histograms, instead of using the famous ggplot2 package, I am using the basic R plotting function.

##--- Creating a Function to simulate 1000 test statistics for two different samples

simulation=function(len_1,len_2){

  A=NULL
  B=NULL
  
  for(i in 1:1000)
  {
    Sam_1=rnorm(len_1,1,sqrt(2))
    Sam_2=rnorm(len_2,1,sqrt(2))
    
    Tn_1=(sqrt(length(Sam_1))*((sum(Sam_1)/length(Sam_1))-1))/sqrt(var(Sam_1))
    
    Tn_2=(sqrt(length(Sam_2))*((sum(Sam_2)/length(Sam_2))-1))/sqrt(var(Sam_2))
    
    A=c(A,Tn_1)
    
    B=c(B,Tn_2)
    
  }
  Mat=as.data.frame(matrix(c(A,B),ncol=2,byrow = F))
  names(Mat)=c("Tn_1","Tn_2")
  return(Mat)
}

X=(simulation(50,1000)) # Data Table

X[1:10,] # Showing 1st 10 samples of the Data Table

##          Tn_1        Tn_2
## 1   0.8020946  0.20259551
## 2  -0.8509208 -1.40945355
## 3  -0.2805664 -1.05684656
## 4  -0.6615001 -0.44404425
## 5   2.3164142 -0.09538437
## 6  -2.3255364 -0.42208845
## 7  -0.2363790  0.60943958
## 8  -2.8176113 -0.40001562
## 9  -0.2177217 -2.25709292
## 10 -0.0575885  2.26107062

# Writing a message

writeLines(paste(c("Omitting","the","rest","990","values")),sep=" ")

## Omitting the rest 990 values

##--- Histogram of the 1st Sample 

hist(X$Tn_1,
     col="red",
     xlab="Tn",
     ylab="Frequency",
     main="For the Sample 1",
     density = 50)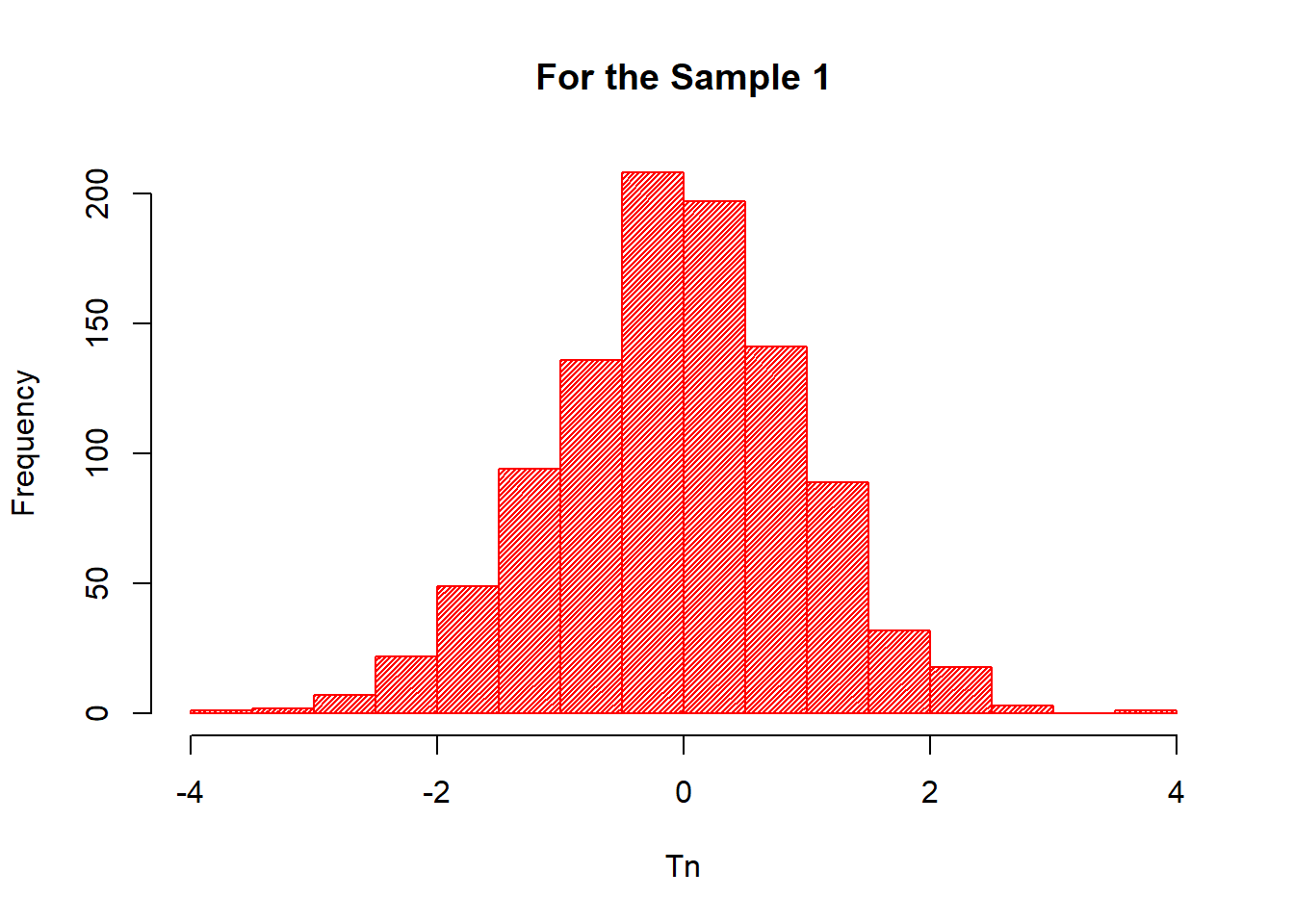

##--- Histogram of the 2nd Sample

hist(X$Tn_2,
     col=12,
     xlab="Tn",
     ylab="",
     main="For the Sample 2",
     density = 40)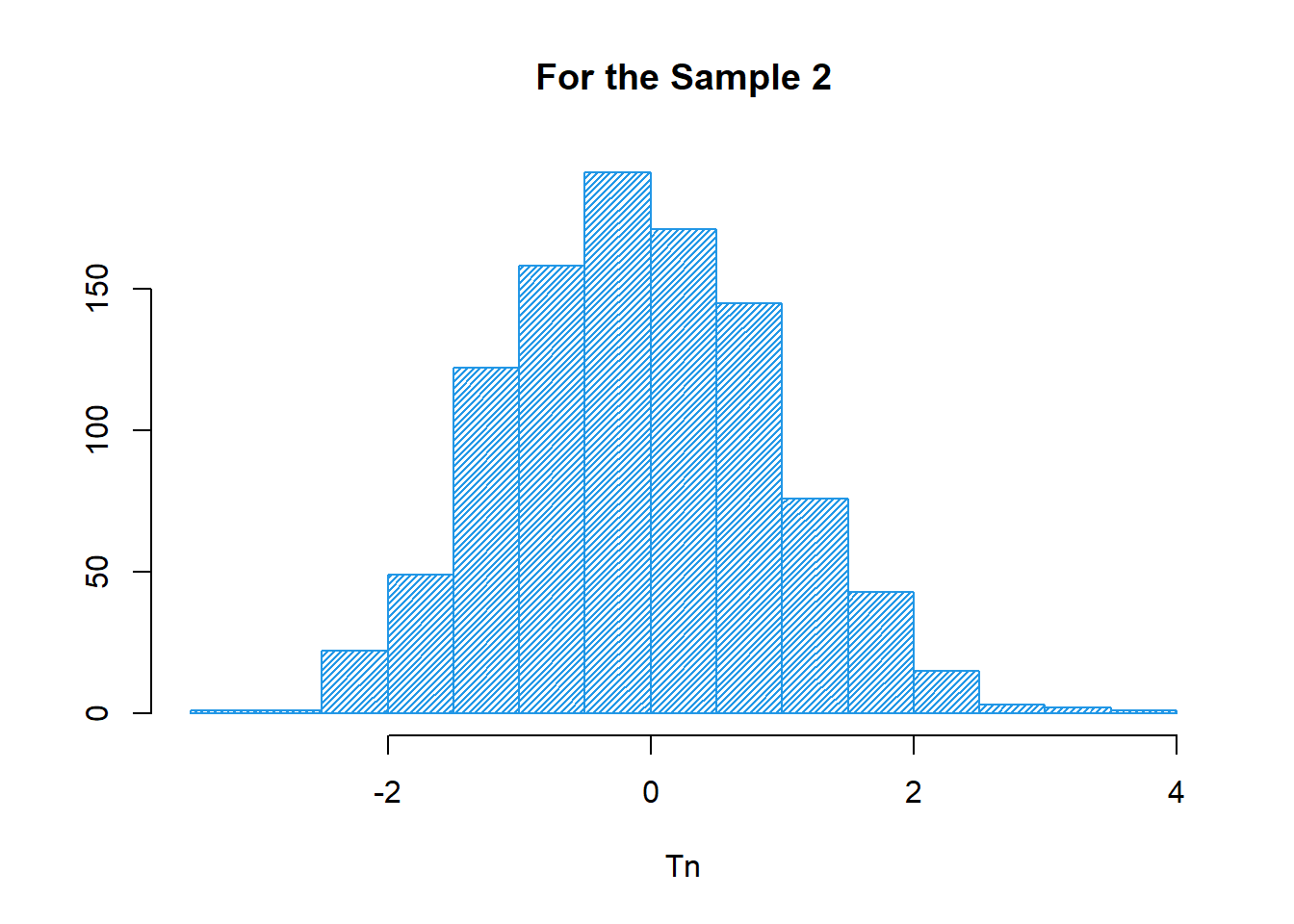

##--- Preparing the density of the N(0,1)

a=seq(-3,3,by= 0.01) # Range of the sample points for N(0,1)

b=dnorm(a) # density of the N(0,1) for the above range.

##--- Comparing Plots :

hist(X$Tn_1,           # histogram for the Sample 1
     col="red",
      xlab="Tn",
      ylab="Frequency",
      main="Comparing Two Histograms coming from two\n different Samples of the same \nPopulation N(1,2) with the Standard Normal density",
     density = 50,
     axes=F,
     cex=4)
par(new=T)             # For Overlap the new plot
hist(X$Tn_2,          
      col=12,
      xlab="",
      ylab="",         # histogram for the Sample 2  
      main="",
     density = 40,
     axes = F)
par(new=T)             # For Overlap the new plot
plot(a,b,
     type ="l",
     xlab="",
     ylab="",          # Density curve of the N(0,1)
     main = "",
     axes = F, 
     col="darkgreen",
     lwd=3)

# Adding Legend

legend("topright",        
       legend = c("Sample 1","Sample 2","PDF-N(0,1)"),
       fil=c("red",20,"darkgreen"),
       cex=0.6)

# Adding box

box()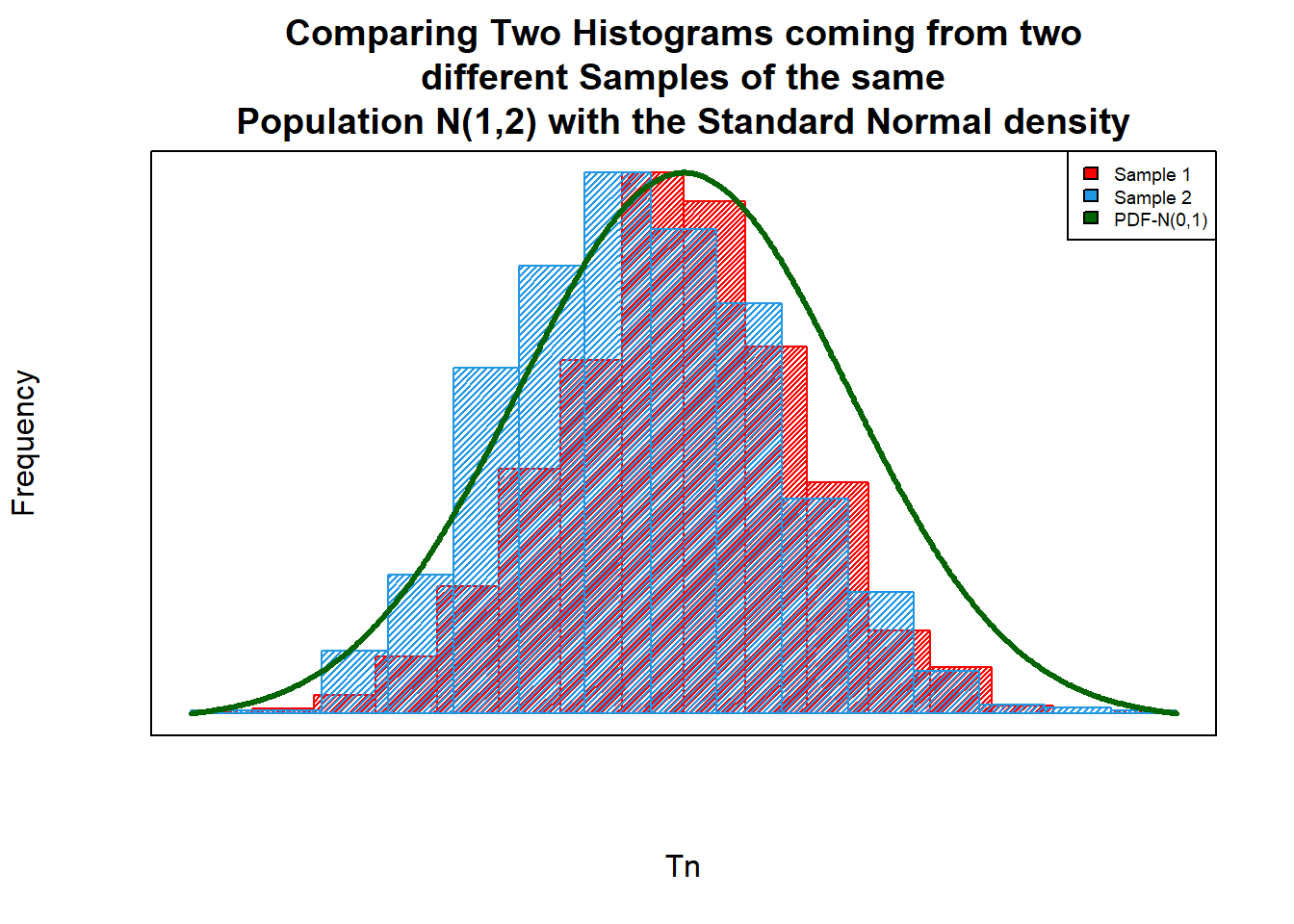

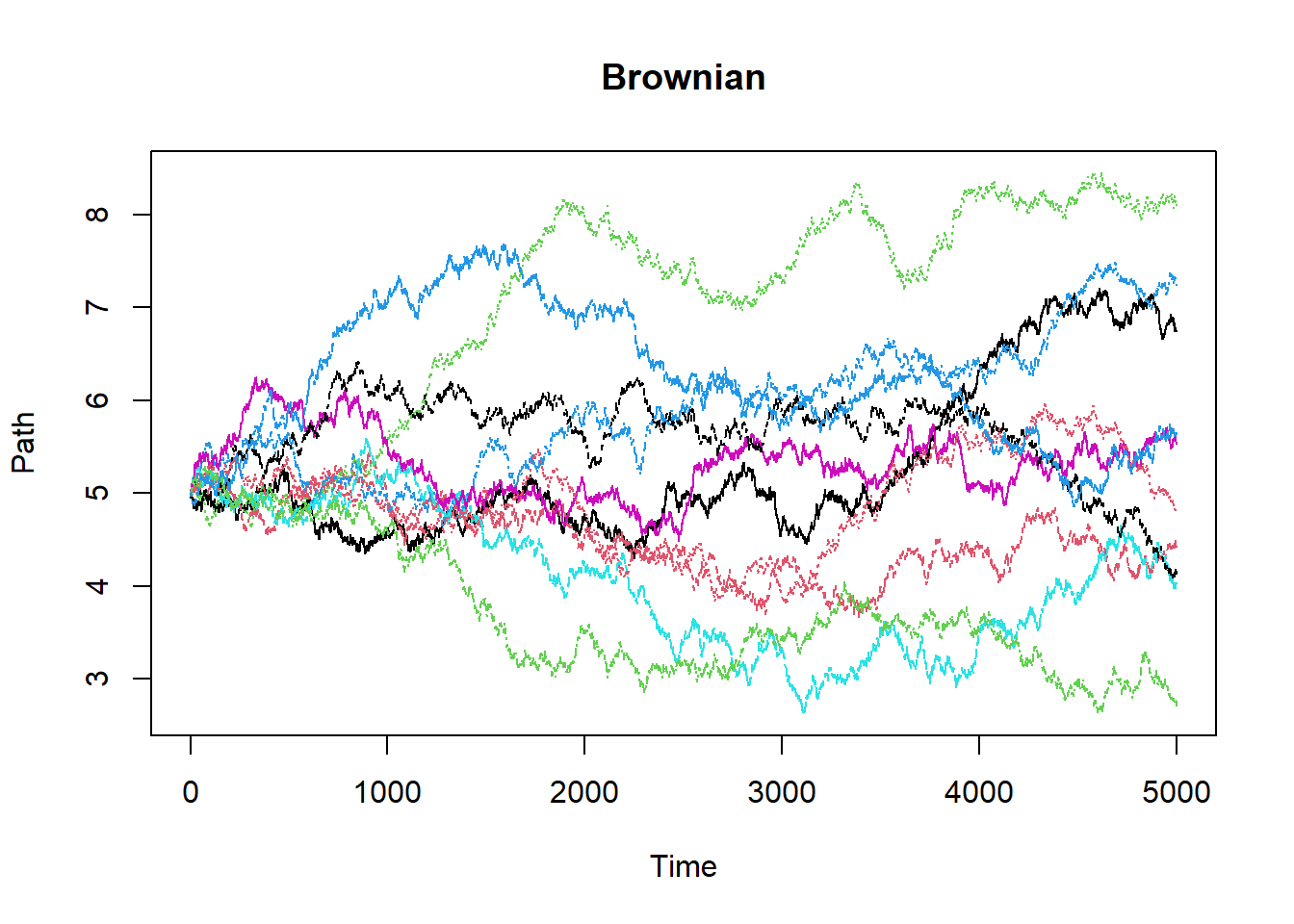
Brownian Motion

• Note that the concepts on basics of Monte Carlo Simulation and various Random Distributions have been introduced lets focus on using Monte Carlo methods to simulate paths for various Stochastic Processes.

• Standard Brownian Motion on $[0,T]$ is a Stochastic Process $(W(t),0\le t\le T)$ which satisfies some properties such as

  • $W(0)=0$
  • For any $k$ and any $0\le t_1\le ....\le T$, the increments between any two successive $W(t_i)-W(t_{i-1})$ are independent.
  • The difference $W(t)-W(s)\sim N(0,t-s)$ for any $0\le s<t\le T$

As a consequence of 1st and 2nd, $W(t)\sim N(0,t)$.

On the other hand, Brownian Motion which is non-standard will have two parameters just like Normal Distribution known as drift and diffusion. Using $W(t)$ we therefore give a Stochastic Differential Equation for any Brownian Motion

$$Brownianmotionwithdrift\mu anddiffusioncoefficient{\sigma }^{2}throughtheSDE$$ $$dX(t)=\mu (t)dt+\sigma (t)dW(t)$$

Sample Paths Generations

Solving the SDE presented above we can write the equation in terms of $X(t_i),\mu (s),\sigma (s)$ $$X(t_{i+1})=X(t_i)+{\int }_{t_i}^{t_{i+1}}\mu (s)ds+\sqrt{{\int }_{t_i}^{t_{i+1}}{\sigma }^2(u)du{Z}_{i+1}}$$ Hence let us look at the code to generate paths where I have assumed $\mu$ and $\sigma$ to be constant.

Brownian = function() # This is a function to generate Browninan with drift 0.04 and diffusion 0.7
{
    paths = 10
    count = 5000
    interval = 5/count
    sample = matrix(0,nrow=(count+1),ncol=paths)
    for(i in 1:paths)
    {
        sample[1,i] = 5
        for(j in 2:(count+1))
        {
            sample[j,i] = sample[j-1,i]+interval*0.04+((interval)^.5)*rnorm(1,0,1)*0.7
        }
    }   
    cat("E[W(2)] = ",mean(sample[2001,]),"\n")
    cat("E[W(5)] = ",mean(sample[5001,]),"\n")
    matplot(sample,main="Brownian",xlab="Time",ylab="Path",type="l")
}

StandardBrownian = function() # This is a function to generate Standard Browninan with drift 0 and diffusion 1
{
    paths = 10
    count = 5000
    interval = 5/count
    sample = matrix(0,nrow=(count+1),ncol=paths)
    for(i in 1:paths)
    {
        sample[1,i] = 0
        for(j in 2:(count+1))
        {
            sample[j,i] = sample[j-1,i]+((interval)^.5)*rnorm(1)
        }
    }   
    cat("E[W(2)] = ",mean(sample[2001,]),"\n")
    cat("E[W(5)] = ",mean(sample[5001,]),"\n")
    matplot(sample,main="Standard Brownian",xlab="Time",ylab="Path",type="l")
}
StandardBrownian()

## E[W(2)] =  -0.2205643 
## E[W(5)] =  -0.2023842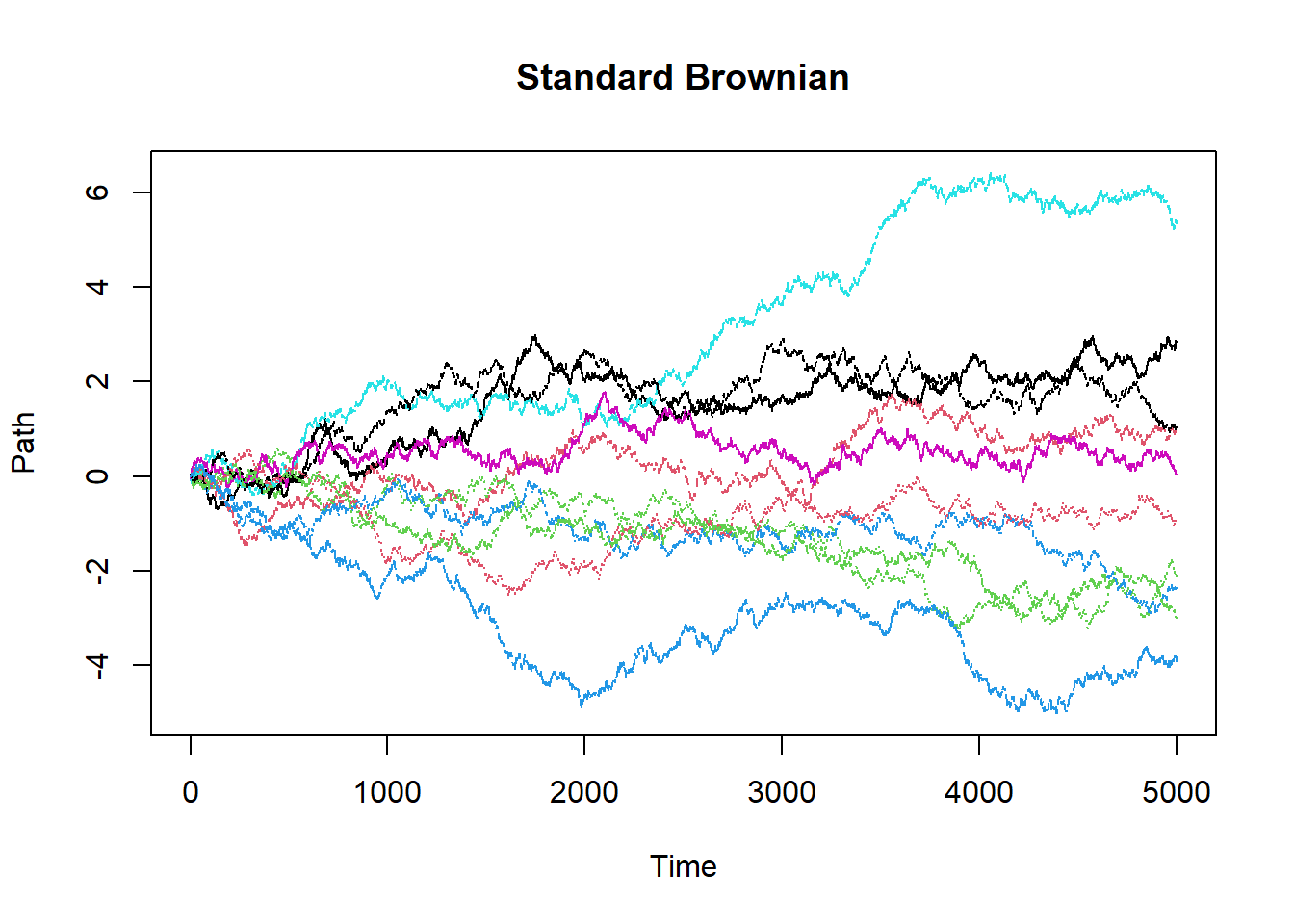

Brownian()

## E[W(2)] =  5.321014 
## E[W(5)] =  5.338038